Tau(q) exercises

Recall that if all the scaling factors ri take on a common value, r, the tau(q) equation can be solved explicitly:

tau(q) = -ln(p1q + ... + pNq)/ln(r).

As an illustration, take these values: r = 0.5, p1 = 0.05, p2 = 0.2, p3 = 0.3, and p4 = 0.45, we compute some points on the tau(q) curve.

Fill in the tau(q) values for this table.

q	tau(q)
-2
-1
0
1
2
5

Plot these points and sketch the tau(q) curve. Here are the completed table and the graph.

As another illustration take these values: r = 0.5, p1 = 0.20, p2 = 0.25, p3 = 0.30, and p4 = 0.35, we compute some points on the tau(q) curve.

Fill in the tau(q) values for this table.

q	tau(q)
-2
-1
0
1
2
5

Plot these points and sketch the tau(q) curve. Here are the completed table and the graph.

From these graphs, comment on

(1) limq -> infinity tau(q) and limq -> -infinity tau(q)   Answer

(2) The graph of tau(q) is decreasing.   Answer

First inspect a tau(q) graph, then prove the graph decreases using the the calculation

dtau/dq = -( 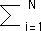piqritau(q)(ln(pi))/( 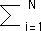piqritau(q)(ln(ri))

(You may wish to begin with the special case of all ri = r. Simplify the formula for dtau/dq in this case.)

(3) The graph of tau(q) is concave up.   Answer

First inspect a tau(q) graph, then prove the graph opens upward using the the calculation

d2tau/dq2 = -( 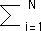piqritau(q)(ln(pi) + (dtau/dq)ln(ri))2)/( 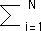piqritau(q)(ln(ri)))

(You may wish to begin with the special case of all ri = r. Simplify the formula for d2tau/dq2 in this case.)

(4) The graph of tau(q) has oblique asymptotes. Assuming these asymptotes pass through the origin, estimate the slopes of these asymptotes Try taking larger (that is, more positive and more negative) values of q.   Answer

Return to Multifractals.