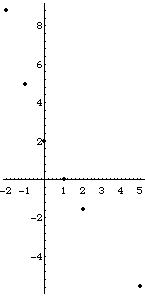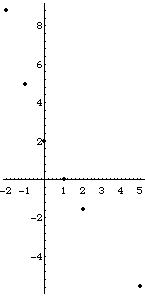| Pictured here are some points on the tau(q) graph for these values:
r = 0.5, p1 = 0.05,
p2 = 0.2, p3 = 0.3, and
p4 = 0.45. |
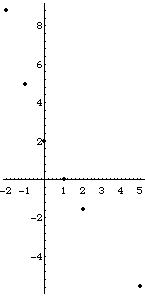 |
| Inspection of the graph certainly suggests that the graph of tau(q) is decreasing. |
| |
| Recall the the calculation |
| dtau/dq = -( | 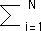 |
piqritau(q)(ln(pi)) / ( |
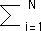 |
piqritau(q)(ln(ri)) |
|
| In the special case that all ri = r, this simplifies to |
| dtau/dq = -( | 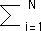 |
piq(ln(pi)) / (ln(r) |
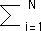 |
piq) |
|
| Because 0 < r < 1, ln(r) < 0 and so the denominator is negative. |
| Because each 0 < pi < 1, ln(pi) < 0 and so
each term of the numerator is negative. |
| Then the minus in front of the fraction gives dtau/dq < 0. That is, the
graph of tau(q) is decreasing. |
| The general case of distinct ri follows by noting that each 0 < ri < 1,
so each ritau(q) > 0 and each ln(ri) < 0.
Then each term of the denominator is negative and each term of the numerator is negative. |