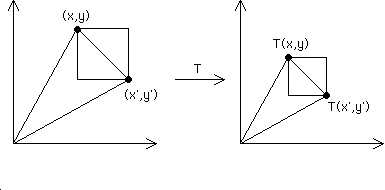
| A contraction is a transformation T that reduces the distance between every pair of points. |
| That is, there is a number |
| dist(T(x, y), T(x', y')) ≤ r⋅dist((x, y), (x', y')) |
| for all pairs of points (x, y) and (x', y'). |
| Here dist denotes the Euclidean distance between points: |
| dist((x, y), (x', y')) = ((x - x')2 + (y - y')2)1/2 |
| To save space we write dist((x, y), (x', y')) = d((x, y), (x', y')). |
| The contraction factor of T is the smallest r satisfying |
| d(T(x, y), T(x', y')) ≤ r⋅d((x, y), (x', y')) |
| for all pairs of points (x, y), (x', y'). |
 |
| In general, contractions can reduce distances between points by different amounts, depending on the position of the points. |
| Here are some special kinds of contractions. |
| A similarity reduces all distances by the same number,
|
| d(T(x, y), T(x', y')) = r⋅d((x, y), (x', y')) |
| for all pairs of points (x, y), (x', y'). |
| The transformation T(x, y) = (r⋅x, r⋅y) is an example; its contraction factor is r. |
| An affinity reduces distances by different amounts in different directions. For example, |
| T(x, y) = (r⋅x, s⋅y), |
| where both r < 1 and s < 1, and r and s are different. |
| What is the contraction factor for the affinity T(x, y) = (x/2, y/3)? here is the Answer. |
| If all the transformations of an IFS are contractions, then iterating the IFS is guaranteed to converge to a unique shape. |
Return to IFS Convergence.