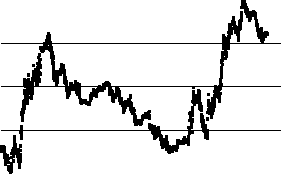
| Here are the successive differences of the cartoon data. Note most differences
lie in bin2 and very few in bin1, bin3, and bin4. |
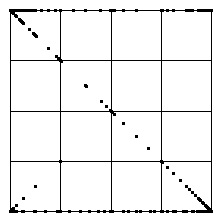
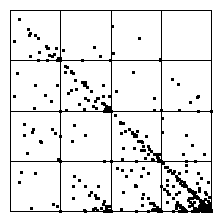
Here is the IFS driven by these differences as data points.
Most of the IFS points cluster near (1,0), the result of most of the data points
lying in bin2. Along the bottom of the square, note the clusters of IFS points
at (1/2,0), (3/4,0), (7/8,0), and (15/16,0).
Almost all the IFS points along the bottom of the square lie in these clusters, indicating that a
long sequence of data points in bin2 can be followed by a single data point in
bin1, followed immediately by more data points in bin2. The less
clustered distribution of IFS points along the line between (1,0) and
(0,1) indicates that data points fall in bin2 and bin3
in more complicated combinations. |