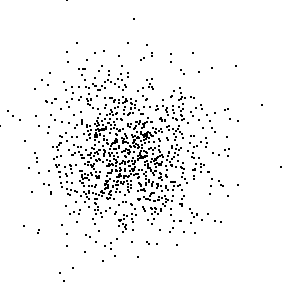
| Brownian motion Y(t) is stationary: the
differences |
| Y(t + h) - Y(t) |
| are independent of t. |
| To illustrate this visually, we sample a Brownian
motion simulation and compute increments |
| incr1 = Y(t1 + h) - Y(t1),
incr2 = Y(t2 + h) - Y(t2),
...,
incr1000 = Y(t1000 + h) - Y(t1000). |
| We must take the ti so ti+1 ≥ ti + h;
if the sampling increments overlap, we should not expect independence. |
| Then we plot the points |
| (incr2, incr1), ...,
(incr1000, incr999). |
| If the increments are
independent of one another, the points should lie in an approximately
circular cloud, denser near the center. |
| The left picture shows such a plot
for h = 1, the right for h = 2. |
|