| Third, repeating a pattern under magnification is not sufficient
to guarantee fractality. |
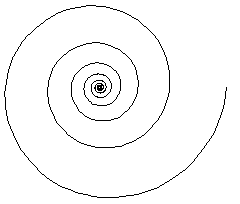
| For example, a spiral (A below) is symmetric under
magnification about its
center point, but about no other point. |
| Iterating this process, the limiting shape is
just a single point. |
| In order to produce a fractal, at each level the decomposition
must involve at least two scaled copies. |
| Nested dolls (often Russian, but not in this instance, B) are another example
of a non-fractal involving a single scaling transformation, as is the cat bottle (C). |
| On the other hand, the cow picture (D) is fractal, as would be
more obvious if the cow's left earring were turned toward us. |
| Thanks to Nial Neger for finding the cat and cow pictures. |
| Click on all but the spiral to magnfy in a new window. |