
 |
 |
| Addresses 2 and 3 appear to have about the same number of points. Addresses 1 and 4 have about the same number of points, and fewer than in addresses 2 and 3. So we think | |
| p2 = p3 > p1 = p4 | |
| Because r1 = r2 = r3 = r4, the minimum probability corresponds to the maximum α, and the maximum probability corresponds to the minimum α. | |
| Then | |
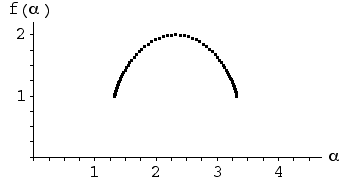
| The maximum probability occurs when just the transformations T2 and T3 are applied. These generate the line between corners 2 and 3, so this line fills in most densely, which we observe. Then f(αmin) is the dimension of the line between corners 2 and 3, that is, f(αmin) = 1. We see this on the left endpoint of the f(α) curve. | |
| The minimum probability occurs when just the transformations T1 and T4 are applied. These generate the line between corners 1 and 4, so this line fills in least densely, which we observe. Then f(αmax) is the dimension of the line between corners 1 and 4, that is, f(αmax) = 1. We see this on the right endpoint of the f(α) curve. | |
| The four transformations T1, T2, T3, and T4 generate the filled-in unit square, a 2-dimensional shape. consequently max(f(α)) = 2. We see this as the highest point of the f(α) curve. | |
Return to visual interpretations of f(α) curves.