Multifractals

Dimension of the attractor

Recalling df/dalpha = q, we see the only critical point of f(alpha) occurs at q = 0.

Because the graph of f(alpha) is concave down, the maximum value of f(alpha) occurs at q = 0.

Substituting q = 0 into

p1qr1tau(q) + ... + pNqrNtau(q) = 1

the equation defining tau(q),

we obtain

r1tau(0) + ... + rNtau(0) = 1

We recognize this is the Moran equation for the dimension, d, of the attractor, with d = tau(0).

Recalling f(alpha) = q*alpha + tau(q), we see that q = 0 gives

f(alpha) = tau(0) = d

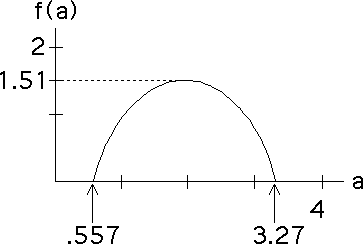
That is, the maximum value of f(alpha) gives the dimension of the attractor.

To emphasize the point that the maximum value of the f(a) curve is the dimension of the underlying fractal, suppose we change the four transformations so they all have scaling factors 0.4.

The dimension of the fractal is Log(4)/Log(1/.4) = 1.51.

Return to Multifractals from IFS.