|
By a simple change of variables, the familiar
logistic map
xn+1 = sxn(1 - xn), can be recoded into to form
xn+1 = xn2 + c. Note the similarity with the
Mandelbrot set iteration formula.
|
| Letting c range from c = 1/4 to c = -2, generate the sequence of
numbers x0 = 0,
x1 = x02 + c,
x2 = x12 + c, ... . Plot
c along the horizontal axis, and in the vertical line above each c value, plot
x100 through x200.
|
| For -3/4 < c < 1/4,
the values xi converge to a fixed point, whose value depends on c, decreasing
as c decreases.
|
| For -5/4 < c < -3/4, the values xi converge
to a 2-cycle. And so on.
|
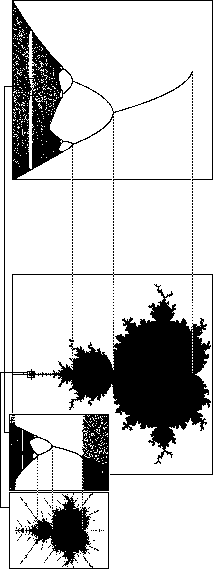
| Plotting all these eventual behaviors together
for -2 < c < 1/4 gives the bifurcation diagram for the
recoded logistic map xn+1 = xn2 + c. This is the
top of the figure on the right.
|
| Note from the insert that the logistic bifurcation diagram has
fracal characteristics: it is filled with small copies of itself.
|
| From the branching structure of the logistic bifurcation
diagram we can read the cycle number of the corresponding features of the
Mandelbrot set.
|
| So all the interesting dynamics of the logistic map are contained in
the middle section of the Mandelbrot set (the part along the real axis).
|