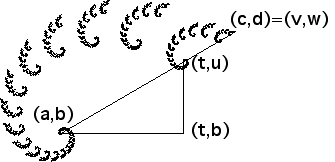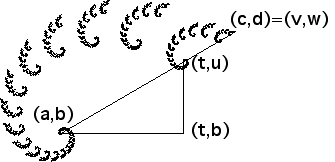Spiral Fractals from IFS

Sample

This spiral is decomposed into two pieces: the right-most spiral and everything else. Because this is a self-similar fractal, we need find only r, theta, e and f for both pieces.

Right-most spiral Select points (a,b) and (c,d) on the whole spiral. The corresponding points on the right-most spiral are (t,u) and (v,w).

r We measure 55mm for dist((a,b),(c,d)) and 16mm for dist((t,u),(v,w)). Consequently, r = 16/55 = 0.29. Because the shape is self-similar, s = r = 0.29.

theta The line (t,u) to (v,w) is parallel to the line (a,b) to (c,d). So θ = 0. Because the rotation is without distortion, φ = θ.

e The horizontal distance from (a,b) to (t,u) is 35mm. As a scale we take the horizontal distance from (a,b) to (c,d), measured as 49mm. So e = 35/49 = 0.71.

f The vertical distance from (a,b) to (t,u) is 20mm. We must use the same scale for all vertical and horizontal translations, so f = 20/49 = 0.41

Everything else Here are the points (t,u) and (v,w) for this piece.

r We measure 55mm for dist((a,b),(c,d)) and 46mm for dist((t,u),(v,w)). Consequently, r = 46/55 = 0.84.. Because the shape is self-similar, s = r = 0.84.

theta The line (t,u) to (v,w) makes an angle of about 20 deg with the line (a,b) to (c,d). So theta = 20. Because the rotation is without distortion, phi = theta.

e The horizontal distance from (a,b) to (t,u) is 0mm, so e = 0.

f The vertical distance from (a,b) to (t,u) is 0mm, so f = 0.

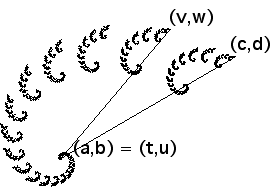
Probabilities Visual inspection of the right-most spiral suggests it occupies about 10% of the whole spiral. So we guess

p₁ = 0.1, and consequently p₂ = 0.9

Alternately, we compute

p₁ = r₁²/(r₁² + r₂²) = .29²/(.29² + .84²) = 0.11

and consequently p₂ = 1 - 0.11 = 0.89.

Here is the IFS table for this spiral.

	r	s	θ	φ	e	f	prob
T1	0.29	0.29	0	0	0.71	0.41	0.11
T2	0.83	0.83	20	20	0	0	0.89

Return to Spiral Fractals from IFS