Fractal Folds Lab Answers

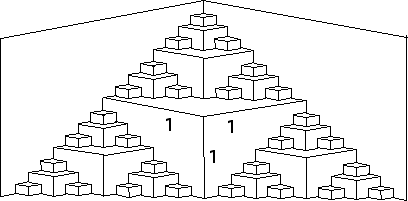
3. First approach. Refer again to the picture to see that the shape is made up of a collection of cubes.

Here is a tabulation of the cubes.

step	number of cubes	cube side length
1	1	1
2	3	1/2
3	9	1/4
4	27	1/8
	...
n	3n-1	1/2n-1

So the total volume is

1 + 3(1/2)³ + 9(1/4)³ + 27(1/8)³ + ... + 3^n-1(1/2^n-1)³ + ...

= 1 + 3/8 + (3/8)² + (3/8)³ + ...

The sum is a geometric series with ratio 3/8, hence it converges to 1/(1 - (3/8)) = 8/5.

Second approach. Note the whole shape consists of a cube of side length 1, together with three smaller copies of the shape - one red, one green, and one blue - each shrunk by 1/2 in each direction.

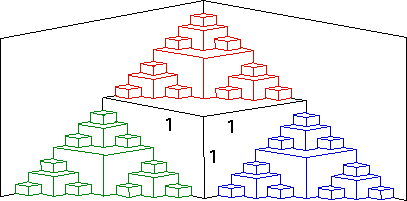Consequently, the three small copies have volume 1/8 the volume of the whole shape.

Say the volume of the whole shape is x. Then we see

x = 1 + 3(x/8)

We know x is finite, because the entire shape is contained in a cube of side length 2. Consequently, we can solve this equation for x, obtaining x = 8/5.

Return to PaperFolding Lab.