Fractal Folds

Background

Fat Cantor Set

The second fractal fold is based on a variation on this Cantor set: we use the same procedure but vary the sizes of the pieces removed.

First, remove the middle 1/4 of the unit interval.

From each of the remaining two pieces remove an interval of length 1/16 = 1/4².

From each of the remaining four pieces remove an interval of length 1/64 = 1/4³.

and so on.

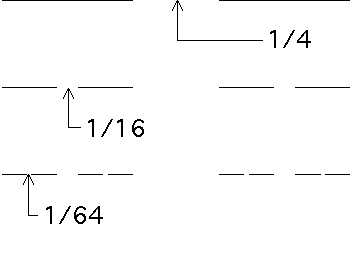
The lengths of the gaps for the first three stages of a fat Cantor set.

The sum of the lengths of the removed intervals is

S = 1/4 + 2(1/16) +4(1/64) + 8(1/256) + ... = 1/4 + 1/8 + 1/16 + 1/32 + ...

This is a geometric series with first term 1/4 and ratio 1/2, and so

S = (1/4)/(1 - 1/2) = 1/2.

Roughly, the process has not removed all the length of the initial segment; more precisely, this Cantor set has positive measure. Yet this set is still uncountable and also contains no intervals.

Cantor's original set was the middle thirds set.

Today any set made by iteratively removing middle portions is called a Cantor set. All are fractals: any subset contains scaled copies of the entire set.

Mandelbrot has given these sets the evocative name fractal dusts.

Positive measure Cator sets are examples of fat fractals.

Mandelbrot conjectures that radial cross-sections of Saturn's rings are fat Cantor sets. For supporting evidence, click each picture for an enlargement in a new window.

A Voyager picture of Saturn	A (false color) Voyager closer view of Saturn's rings

Return to Background