Convergence of Deterministic IFS

Consider the transformations

T₁(x, y) = (x/2, y/2),

T₂(x, y) = (x/2, y/2) + (1/2, 0), and

T₃(x, y) = (x/2, y/2) + (0, 1/2).

These generate a right isosceles Sierpinski gasket.

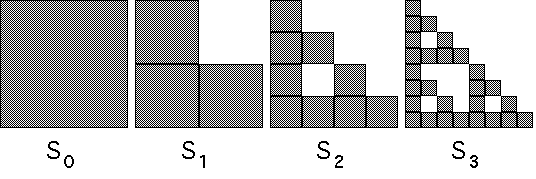
Start with the unit square S₀. Then

S₁ = T₁(S₀) U T₂(S₀) U T₃(S₀),

S₂ = T₁(S₁) U T₂(S₁) U T₃(S₁),

S₃ = T₁(S₂) U T₂(S₂) U T₃(S₂),

and so on. Here are S₀ through S₃, arranged side-by-side.

To make precise the sense in which S_n converge, we compute the Hausdorff distances

First, h(SO,S1) = 1/2

Next, h(S1,S2) = 1/4

Then, h(S2,S3) = 1/8

In general, h(Sn-1,Sn) = 1/2n

Return to Convergence of determinisitc IFS.