Driven IFS with Forbidden Combinations

T₄ never occurs

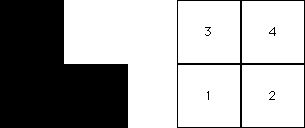
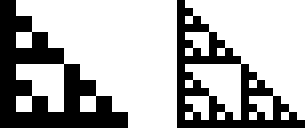
If T4 is never applied, then no points land in the subsquare S4 with address 4. That is, the upper right subsquare is completely empty.

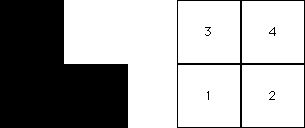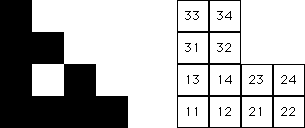
Because the subsquare S4 contains no points, the subsquares T1(S4) = S14, T2(S4) = S24, and T3(S4) = S34 contain no points.

Continuing, the subsquares T1(S14) = S114, T1(S24) = S124, T1(S34) = S134, ..., and T3(S34) = S334 contain no points. That is,

if i=4, j=4, or k=4, the subsquare Sijk contains no points (below left).

Similarly,

the subsquare Sijkm contains no points if any of i, j, k, or m is 4 (below right).

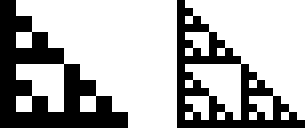The result of continuing this process is clear:

if T4 is never applied, every square whose address contains a 4 is empty.

With this restrction, we see the IFS generates a right isosceles Sierpinski gasket. This is no surprise, because the IFS {T1, T2, T3} generates a right isosceles Sierpinski gasket.

Return to Driven IFS with forbidden combinations.