Box-Counting Dimension of a Filled-in Triangle

Plot the points

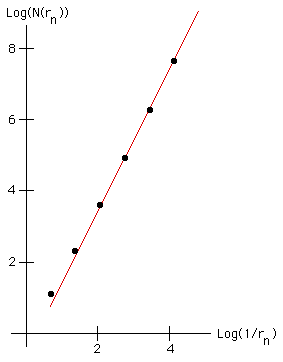
(Log(1/r0),Log(N(r0))) = (Log(1), Log(1)) = (0, 0) (Log(1/r1),Log(N(r1))) = (Log(2), Log(3)) ≈ (0.301, 0.477) (Log(1/r2),Log(N(r2))) = (Log(4), Log(10)) ≈ (0.602, 1.0) (Log(1/r3),Log(N(r3))) = (Log(8), Log(36)) ≈ (0.903, 1.556) (Log(1/r4),Log(N(r4))) = (Log(16), Log(136)) ≈ (1.204, 2.134) ...

(the graph shows a greater range, and more widely spaced, points than these) and see if they lie approxiamtely on a straight line of slope 2.

Indeed, the points do appear to lie approximately along a straight line of slope 2. The fit is not perfect because the squares cover more than the triangle.

Return to Box-Counting Dimension of a Filled-in Triangle.