| We have seen that points of an
n-cycle of L(x) are fixed points of Ln(x). So we
look at graphs of some compositions of the logistic map for various
s-values. |
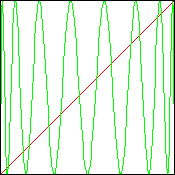
| Here we see the s = 4 pictures for
L2(x), L3(x), and L4(x). Click on each
picture for an animation of s going from 2 to 4 in steps of 0.25. Click an animation to stop. |
|
| A careful comparison of these three animations reveals cycles
arise in two different ways, illustrated by these observations. |
| The 2-cycle appears where one of the
fixed points of L(x) becomes unstable, |
| but the 3-cycle seemss to appear from nothing. |
|
| Maybe the difference has to do with even and odd cycles. |
| No, looking at the 4-cycle animation shows two 4-cycles: |
| the first appears where the 2-cycle becomes unstable, |
| the second arises from nothing. |
|
| In fact, these are the two mechanisms for producing
new cycles. The first is called a
period-doubling bifurcation, the second a
tangent bifurcation. |
| Here is a brief description of the geneology
of cycles. |