Julia Sets and the Mandelbrot Set
Complex Newton's Method
Derivation of the Newton's Method Formula
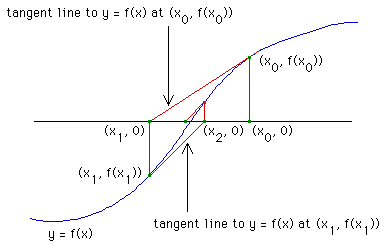
We derive the relation between x1 and x0;
the others are similar. Note the points (x0, f(x0)) and
(x1, 0) lie on the line tangent to the graph of y = f(x) at
the point (x0, f(x0)). The slope of the tangent
line is f '(x0), so we have
f '(x0) = (f(x0) - 0) / (x0 - x1)
Solving this for x1 gives
x1 = x0 - f(x0)/f '(x0)
Return to
Complex Newton's Method