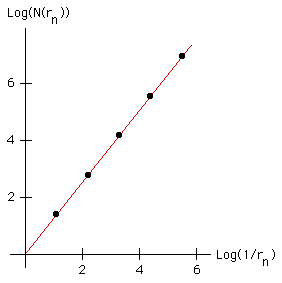Box-Counting Dimension of the Koch curve

Plotting the points

(Log(1/r0),Log(N(r0))) = (Log(1), Log(1)) = (0,0) (Log(1/r1),Log(N(r1))) = (Log(3), Log(4)) = (0.477, 0.602) (Log(1/r2),Log(N(r2))) = (Log(9), Log(12)) = (0.954, 1.079) (Log(1/r3),Log(N(r3))) = (Log(27), Log(48)) = (1.431, 1.681) (Log(1/r4),Log(N(r4))) = (Log(81), Log(192)) = (1.908, 2.283) ...

(the graph shows a greater range, and more widely spaced, points than these) we see they lie on a straight line of slope about 1.26.

So the box-counting dimension of the Koch curve is about 1.26.

Return to Box-Counting Dimension of the Koch curve.