Area-Perimeter Relation: Fractal Problems

A first attempt to extend the Euclidean area-perimeter relation P = k⋅Ad/2 to shapes with fractal perimeters would be to simply replace the Euclidean d = 1 with the dimension of the fractal perimeter.

To see why this cannot work, consider this illustrative example.

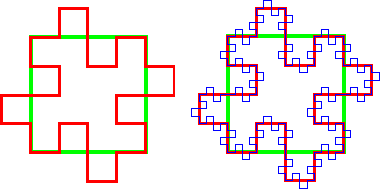
Start with the unit square. Take each side to be a initiator and replace it with the 8-segment generator.

Note that each of the four copies of the generator adds as much to the enclosed area as it removes, so the shape enclosed on the left has area 1.

On the right we superimpose the second iteration.

Continuing to the limit we produce a fractal curve that encloses a region of area 1. What are the dimension and length of this curve?

Dimension is sraightforward. From the pattern begun with the generator, we see each of the four sides of the limiting curve is made of N = 8 copies, each scaled by a factor of r = 1/4. Consequently, the similarity dimension of the perimeter is

ds = Log(N)/Log(1/r) = Log(8)/Log(4) = Log(23)/Log(22) = 3/2

We know that the length (1-dimensional measure) of an object of dimension d > 1 is infinite, but let's carry out the calculation to reinforce this result.

P(square) = 4⋅1, P(gen 1) = 4⋅8⋅(1/4) = 4⋅2, P(gen 2) = 4⋅82⋅(1/4)2 = 4⋅22

The pattern is clear:

P(gen n) = 4⋅2n

So Length(P(gen n)) → ∞ as n → ∞.

Because the perimeter is infinite and the area is 1, the relation P = k⋅Ad/2 cannot hold.

Return to the area-perimeter relation.