Circle Inversion Fractals

Overlapping Circles Inversion Relations

We begin with a lemma.

Lemma If the open discs D_i bounded by the inverting circles C_i are pairwise disjoint, the only relations among the inversions are I_i² = identity.

Proof Suppose some relation I_i1...I_in = identity holds.

Take a point z₀ in the complement of the closed discs corresponding to the D_i. Then

z1 = Ii1(z0) lies in Di1,

z2 = Ii2(z1) lies in Di2,

... , and

zn = Iin(zn-1) lies in Din.

The hypothesized relation implies z_n = z₀, impossible because z₀ lies outside all the D_i and z_n lies in D_in.

Now we are ready for the theorem.

Theorem Distinct circles C₁ and C₂ intersect with tangents making an angle of (m/n)180, 0 < m < n, if and only if the corresponding inversions I₁ and I₂ satisfy (I₁ I₂)ⁿ = identity.

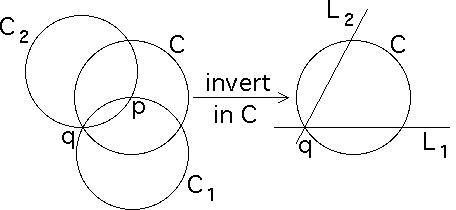
Proof Suppose C₁ and C₂ intersect at two points, p and q.

Denote by C the circle with center p and passing through q.

Because C₁ and C₂ both pass through the center of C, inverting in C transforms C₁ and C₂ into lines (inversion property (vii)) L₁ and L₂, intersecting at q.

Inversion in C transforms the inversions in C₁ and C₂ into the reflections R₁ across L₁ and R₂ across L₂.

Because inversion preserves angles, the angle between L₁ and L₂ at q equals the angle between the tangents of C₁ and C₂ at q.

It is well-known that the composition of two reflections across lines intersecting at a point q is the rotation, about q, through twice the angle between the lines.

For example, in the situation illustrated above, reflection across L₁ is

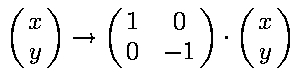and reflection across L₂ is

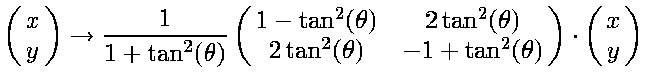where q is the angle between L₁ and L₂.

Reflection across L₁ followed by reflection across L₂ reduces to

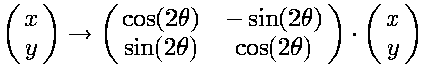That is, rotation by 2q.

If the angle between L₁ and L₂ is (m/n)180, then (R₁R₂)ⁿ is the rotation by n(2m/n)180, that is, the identity.

Using inversion in C to translate this relation back to I₁ and I₂, we see (I₁I₂)ⁿ = identity.

If C₁ and C₂ intersect tangentially at a point p, inversion in a circle C centered at this point p transforms C₁ and C₂ into lines L₁ and L₂ and inversion in C_i into reflection R_i across L_i.

Because the lines are distinct, no relation of the form (R₁R₂)ⁿ = identity holds.

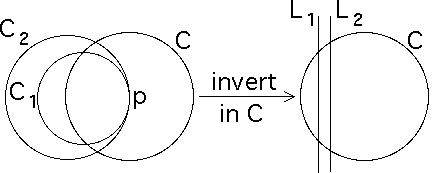Now suppose (I₁I₂)ⁿ = identity.

Then from the Lemma it follows that D₁ and D₂ intersect, consequently C₁ and C₂ intersect in two points, p and q.

(The case C₁ = C₂ is precluded by the hypothesis that the circles are distinct.)

Inverting in the circle C with center p and passing through q transforms the circles C₁ and C₂ into the lines L₁ and L₂, and transforms I₁ and I₂ into reflections R₁ and R₂ across L₁ and L₂.

Denote by q the angle of intersection of L₁ and L₂ at q.

Then as we saw above, R₁R₂ is rotation by 2q, and (I₁I₂)ⁿ = identity implies n2q = m360, so q = (m/n)180.

Return to Overlapping Circles.