The Moran Equation

Unique Solution

To show the Moran equation

1 = r₁^d + ... + r_N^d.

has a unique solution, assuming 0 < r₁ < 1, ..., and 0 < r_N < 1, consider the function

f(d) = r₁^d + ... + r_N^d.

First, note

f(0) = r₁⁰ + ... + r_N⁰ = 1 + ... + 1 = N.

Second, note

f(d) → 0 as d → ∞.

This is because each r_i satisfies 0 < r_i < 1, so

each r_i^d → 0 as d → ∞.

Third, the graph of f(d) is strictly decreasing.

To see this, observe the derivative is

f '(d) = r₁^dln(r₁) + ... + r_N^dln(r_N)

Because 0 < r_i < 1, each ln(r_i) < 0, so f '(d) < 0.

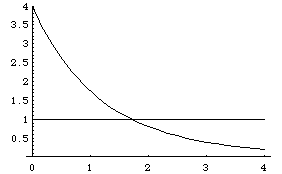
For example, here is the graph of f(d) vs d for N = 4, r₁ = r₂ = r₃ = 1/2, and r₄ = 1/4.

Note that the graph of y = f(d) crosses the horizontal line y =1 at

d = 1.72368... .

We'll see how to find this value in the next section solving the Moran equation.

This is the similarity dimension of a fractal with these scalings.

Return to the Moran equation.